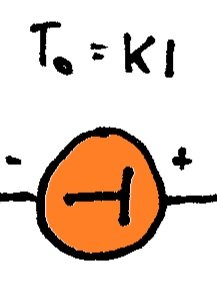The basic Peltier model
A basic Peltier model based on experience
This blog explains a simple model of the Peltier device using electrical elements to represent thermal elements, which has been derived by experiment and found to be highly successful in practice.
At its heart, a Peltier wants to produce a temperature difference which is proportional to the current. This temperature difference can then be used to pump heat or control a temperature. However, there are two limiting factors in the Peltier device itself: the internal thermal resistance, and the effect of the waste heat.
This model shows how these work together and how to calculate the raw potential of a Peltier under optimal conditions, maximum heat pumping and COP estimates. In practice, set ups will have thermal elements outside of the Peltier, which can be expected to reduce the performance, but a good set up will typically achieve 70% of the raw values, so knowing these is a good starting point to sense if a set up is working OK. And the method to calculate the raw power can easily be expanded to include the external elements.
The model can also be used to show why stacked Peltiers are often not a great idea, and also the best way to combine Peltiers to make a more powerful system.
The electrical analogy explained
Analysing a thermal circuit is easily done by using electrical components to represent the thermal elements. The first step in using this approach is to define the thermal elements and their equivalent elements in electrical schematics:
| Thermal characteristic | Electrical equivalent | Units | Notes |
| Temperature | Voltage | K (or °C) | Can be a temperature source or points in the circuit |
| Heat | Current | W (J/s) | Can be a heat source or flowing through the circuit |
| Thermal resistance | Resistance | K/W (°C/W) | Creates a temperature drop when heat flows through the element, just like an electrical resistor |
| Heat capacity | Capacitance | J/K | Not used in the above model, but can exist in a full Peltier system, such as in Al heatsinks or cans of beer |
The electrical analogy is great for people with a basic background in electrical circuits, with simple relations such as V = IR, summation of currents at a node and the ability to set points such as ambient temperatures (ground) or heat sources. However, it’s important not to take this too far. I once spent a couple of hours deep in math trying to optimize the integral of the equivalent of I²R before realizing that it’s not the same thing. Conceptually, both “temperature” and “voltage” are the same in that they provide a pressure to move something, while both electrical and thermal resistance act to restrict the flow in response to the pressure. At this point, it all works nicely. But thermal “heat” and electrical “current” are not the same: one is the flow of pure energy while the other is the flow of just current. Heat can also just flow into or out of an object, while a current in and out of an element must sum to zero. Anyway, take care not to overwork the electrical analogy beyond the simple math!
The heart (To = KI)
The beating heart of a Peltier is the temperature difference that is proportional to the current. The electrical equivalent is a dc voltage source (or a battery). The potential or temperature difference is simply a factor “K” times the current. I’ve modified the normal battery symbol to have a “T” in the middle, but it works the same.
If the K factor is known, the core temperature difference “To” is simply:
To = KI (K or °C)
For a long while, I used a K factor of 20 based on tests with different manufacturers and using K = 20 worked well with simulations matching experiment results. A K factor of 20 means for example a current of 2A will produce a core temperature difference of +40°C or 40K, while 3.5A would produce 70K.
Recently I started using some higher current TEC 12710 (10A type) which were found to have K = 13.5, so some care is needed.
The K factor is unfortunately not shown on datasheets. In principle it could be derived from from some of the graphs in the datasheet, but the numbers don’t always seem to add up. The measurement is best done with relatively low currents such as 0.2A which have negligible waste heat, and using precision temperature loggers with 0.001°C resolution, and squarewave (±200mA) to eliminate the effects of offsets. However even a rough set up with one side of the Peltier on a decent block of metal (grounding that side), the other side open to air or insulated with a temperature sensor, and using say 250mA current and a switch to reverse the polarity should be enough to generate temperature differences of ±5K for a K=20 Peltier. By subtracting the values measured at different polarities, a rough idea of the K factor can be found. For example, if +250mA results in 15.2°C, and -250mA results in 25.2°C then K = (25.2 - 15.2)(0.25 - (-0.25)) = 20.0.
The resistance (Xc, Xh)
The biggest limiting factor of a Peltier is the internal thermal resistance, which is around 1.5 to 2.0 K/W from experiments. Conceptually, if you have say 10W of heat flowing through 1.8 K/W thermal resistance, it will creates a temperature drop of 10 x 1.8 = 18K (or 18°C). This is the same as 10A flowing through 1.8Ω producing a voltage drop of 18V.
At this point, you might think that the maximum power for a Peltier is simply taking the above temperature difference e.g. 60K at 3A, and divide by the resistance (say 1.8 K/W) to get a cooling power of 37.5W. The equivalent electrical analogy would be a 60V battery with 1.8Ω internal resistance, which can produce a maximum of 37.5A. As will be shown in the next steps, this would be wrong as we still need to take into account the effect of the waste heat.
One good thing about the waste heat is that it only flows through the hot side (in typical applications), which is why the model shows the resistance split into two halves, Xc and Xh, which for modelling 40x40mm Peltiers, I typically use 0.9K/W for each half which is based on 0.8K/W for the Peltier itself and 0.1K/W for the coupling resistance.
Since they are the same, in the analysis it can be often just shown as “X”, with the total resistance being 2X.
Unfortunately, Peltier datasheets again fail to identify the thermal resistance despite being a key factor in performance. It can be estimated by the slope of some graphs that show temperature difference vs power at various currents, and it’s best to use the lowest current shown. But again, these graphs can be a bit rubbery.
The waste heat (W = I²R)
As is well known in Peltier land, the waste heat is a big drawback of Peltiers. However, it’s not as bad as many people think, and the way that it works is often misunderstood.
The main TEC 12708 devices I have been working with have an electrical resistance of 1.5Ω so operating at 3A produces a waste of W = 3² x 1.5 = 13.5W
(apologies for using “W” for waste heat which is the same as the units for power!)
Experienced users of Peltiers will probably note that the resistance appears to increase as the system warms up. In reality, this is not so much the resistance changing but the Peltier acting as thermocouple and creating a reverse voltage based on the temperature difference between hot and cold sides. In weak designs, the Peltier has a large temperature difference, so this can result in 20% differences or more. At this point, let’s just assume the Peltier has no temperature difference between hot and cold sides, just to get the lay of the land so to speak. I’ll cover the thermocouple effect in a later blog.
The analysis, step 1: Ta (available temperature)
OK, now we have all the elements it’s time to see how it works. For the purpose of the exercise, let’s use a TEC 12708 with a K factor of 20 (K/A), a thermal resistance of 0.8 K/W for each side, an electrical resistance of 1.5Ω and run it at 3A, so the core temperature is 60K and the waste heat (W = I²R) is 13.5W.
To start the analysis, let’s assume that the hot side of the Peltier is firmly shorted or grounded to ambient (an infinitely large thermal mass), while the cold side is totally insulated. Our target here is to find out what is the available temperature (difference) on the cold side, Ta. This is the electrical equivalent of the open circuit voltage, so this can be referred to as the “open circuit” temperature.
Since the cold side is open, the waste heat only flows through the hot side. In doing so it creates a temperature difference of 13.5 x 0.8 = 10.8K or roughly 11K to keep the numbers simple. This temperature is in the opposite polarity to the 60K created at the Peltier’s core, meaning in effect 49K is now available for pumping. In this example, if the hot side was held at 25°C, the cold side should fall to -24°C.
We can see here that the available temperature difference is the core temperature difference minus [waste heat x thermal resistance of one side]. As a formula:
Ta = KI - WX
= (20 x 3) - (13.5 x 0.8)
= 48.8K
Now, there is some significant stuff here around the waste heat, but for now just note how easy it is to calculate the available temperature difference. Let’s say we wanted to compare “Ta” at different currents, for example 2A, 3A and 4A, it’s pretty easy to do, noting that we have to replace W with I²R as the different currents will affect the waste heat.
using Ta = KI - I²RX:
Ta (@2A) = 20x2 - 2² x 1.5 x 0.8 = 35.2K
Ta (@3A) = 20x3 - 3² x 1.5 x 0.8 = 48.8K
Ta (@4A) = 20x4 - 4² x 1.5 x 0.8 = 60.8K
Note that as we increase the current, the available temperature is not linear. This is because the effect of the waste heat is proportional to current squared. Again, this is an important but different subject that will be dealt with in a separate article.
The analysis, step 2: Pa (available power)
The next step is to simply estimate the available power by also “shorting” the cold side to an infinite thermal mass. We could do this the long way but we are going to use a trick based on the “Thevenin equivalent”: simply divide the available temperature (Ta) calculated above by the total circuit resistance (2X). This means for the TEC 12708 running at 3A:
Pa = Ta / (2X) = 49.2/1.6 = 30.8W
Note that the heat out of the hot side will be Pa plus the waste heat, so 30.8+13.5 = 44.3W
In other words, at 3A we can get 30.5W of cooling and 44W of heat for just 13.5W input, not bad for a device that many experts write off as being hopelessly inefficient. That’s a COP (heating) of 3.3 (330%), not to be laughed at.
The general form for Pa, putting steps 1 and 2 together and replacing I²R for W becomes:
Pa = (KI - I²RX)/(2X)
Or for the TEC 12708 that I use, replacing K = 20, R = 1.5 and X = 0.8 gives:
Pa = (20I - 1.2I²) / 1.6
Using this we can compare the cooling power and COP (heating) at different currents:
@2A: Pa = 22.0W, COPh = 4.67 (Pin = 6.0W)
@3A: Pa = 30.8W, COPh = 3.28 (Pin = 13.5W)
@4A: Pa = 38.0W, COPh = 2.58 (Pin = 24.0W)
We can see that pushing the Peltier harder means we still get more cooling, but the efficiency drops. Keep in mind this analysis uses infinite heatsinks and no outside temperature difference, so these figures will not be achieved in practical set ups. But it is an important step in the analysis of real world applications.
And there’s a rather surprising result is checking the 0.5A value:
@0.5A: Pa = 5.38W, COPh = 15.37 (Pin = 0.375W)
That’s kind of amazing that a Peltier can be over 1500% efficient, when the internet often says it’s just 5% efficient. And before the doubters come, actual experiments have confirmed COPh of over 14 at 0.5A: it’s genuinely amazing experience to see more than 5W of heat being pumped with less than 0.4W input. The catch is that the available temperature difference is small: only 10K. But that’s enough for a butter cooler!